- Autor Matthew Elmers [email protected].
- Public 2023-12-16 22:01.
- Zuletzt bearbeitet 2025-01-24 09:22.

Was bestimmt die Genauigkeit - eines der Hauptmerkmale einer Waffe? Offensichtlich von der Qualität des Laufs und der Patrone. Verschieben wir die Patrone vorerst, aber betrachten wir die Physik des Prozesses.
Nehmen Sie einen Metallstab oder ein Rohr aus elastischem Metall und befestigen Sie es starr in einer massiven Basis. So erhalten wir ein Modell des zu untersuchenden Geräts. Wenn wir nun auf die Stange treffen, ist es egal, an welcher Stelle und in welche Richtung, sie entweder zurückziehen oder zusammendrücken oder schließlich eine Patrone in das Rohr einführen und einen Schuss abfeuern, wir werden sehen, dass die Stange (Fass) ist in eine gedämpfte Schwingbewegung geraten. Diese Vibrationen werden in die einfachsten zerlegt, und jede Art einer solchen einfachen Vibration des Laufs beeinflusst die Genauigkeit (Genauigkeit) des Schießens auf ihre Weise.
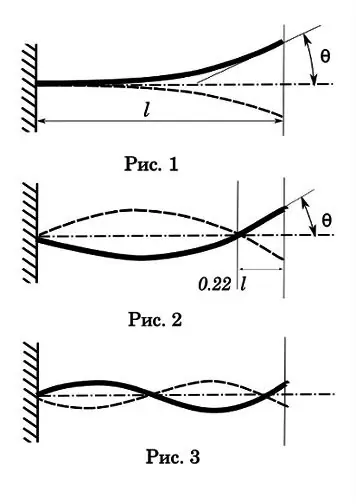
Beginnen wir mit den Schwingungen erster Ordnung oder Tonhöhen. Wie man sieht (Abb. 1) hat eine solche Schwingung nur einen Knoten am Ansatzpunkt, die größte Amplitude, die längste Abklingzeit und die längste Schwingungszeit einer Periode. Diese Zeit beträgt 0,017-0,033 Sekunden. Die Geschosslaufzeit durch die Bohrung beträgt 0, 001-0, 002 Sek. Das heißt, deutlich weniger als der Zyklus einer Schwingung, was bedeutet, dass diese Art von Schwingung keinen signifikanten Einfluss auf die Genauigkeit eines einzelnen Schusses hat. Aber mit automatischer Aufnahme kann ein interessantes Bild entstehen. Nehmen wir an, die Feuerrate beträgt 1200 rds / min, d.h. Zeit eines Zyklus - 0,05 Sek. Bei einer Schwingungsperiode erster Ordnung von 0, 025 s haben wir ein vielfaches Frequenzverhältnis. Und dies ist eine unabdingbare Voraussetzung für die Resonanz mit allen Folgen - die Waffe beginnt so stark zu zittern, dass sie auseinanderfallen kann.
Kommen wir zu Schwingungen zweiter Ordnung (Abb. 2). Aber ich schlage vor, dass Studenten der Geisteswissenschaften zuerst ein Experiment durchführen, um die Defizite der Ausbildung im Bereich der Physik zu beseitigen. Sie müssen einen kleinen Jungen nehmen (Sie können ein Mädchen), ihn auf eine Schaukel stellen und schwingen. Vor dir ist ein Pendel. Stellen Sie sich an die Seite der Schaukel und versuchen Sie, den Jungen mit dem Ball zu treffen. Nach einer Reihe von Versuchen werden Sie zu dem Schluss kommen, dass das Ziel am besten getroffen wird, wenn sich das Ziel in der ersten Schwingungsphase befindet - der maximalen Abweichung vom Gleichgewichtspunkt. An diesem Punkt hat das Ziel die Geschwindigkeit Null.
Schauen wir uns das Diagramm zweiter Ordnung an. Der zweite Schwingungsknoten befindet sich ungefähr 0,22 vom Ende des Laufs entfernt. Dieser Punkt ist ein Naturgesetz, es ist unmöglich, solche Schwingungen für den Kragträger zu erzeugen, so dass der zweite Knoten auf das freie Ende fällt. Es ist, wo es ist und hängt nicht von der Länge des Fasses ab.
Die Schwingungsamplitude für das Schema zweiter Ordnung ist geringer, aber die Schwingungszeit ist bereits mit der Zeit des Durchgangs des Geschosses durch die Bohrung vergleichbar - 0,0025-0, 005 Sek. Für Einzelaufnahmen ist dies also schon von Interesse. Um zu verdeutlichen, wovon wir sprechen, stellen Sie sich ein 1 Meter langes Fass vor. Die Kugel durchläuft den gesamten Lauf in 0,001 Sekunden. Wenn die Schwingungsdauer 0,004 Sekunden beträgt, erreicht der Lauf, wenn das Geschoss den Lauf verlässt, in der ersten Phase seine maximale Biegung. Die Frage für die Geisteswissenschaften lautet: An welchem Punkt (in welcher Phase) ist es am besten, eine Kugel aus dem Lauf zu schießen, um konsistente Ergebnisse zu gewährleisten? Denken Sie an die Schaukel. Am Nullpunkt ist der Vektor der Rumpfauslenkungsgeschwindigkeit maximal. Es ist schwieriger für ein Geschoss, diesen Punkt am Laufschnitt zu treffen, es hat auch seinen eigenen Geschwindigkeitsfehler. Das heißt, der beste Moment für das Ausfliegen des Geschosses ist, wenn sich der Lauf am höchsten Punkt der ersten Auslenkungsphase befindet - wie in der Abbildung. Geringfügige Abweichungen in der Geschossgeschwindigkeit werden dann durch die längere Verweildauer des Laufs in seiner stabilsten Phase ausgeglichen.
Eine grafische Darstellung dieses Phänomens ist im Diagramm (Abb. 4-5) deutlich zu erkennen. Dabei ist t der Zeitfehler, mit dem das Geschoss die Laufmündung kreuzt. In Abb. 4 ist ideal, wenn die durchschnittliche Startzeit des Geschosses mit der Nullphase der Laufschwingung zusammenfällt. (Mathematiker! Ich weiß, dass die Geschwindigkeitsverteilung nichtlinear ist.) Der schattierte Bereich ist der Ausbreitungswinkel der Bahnen.
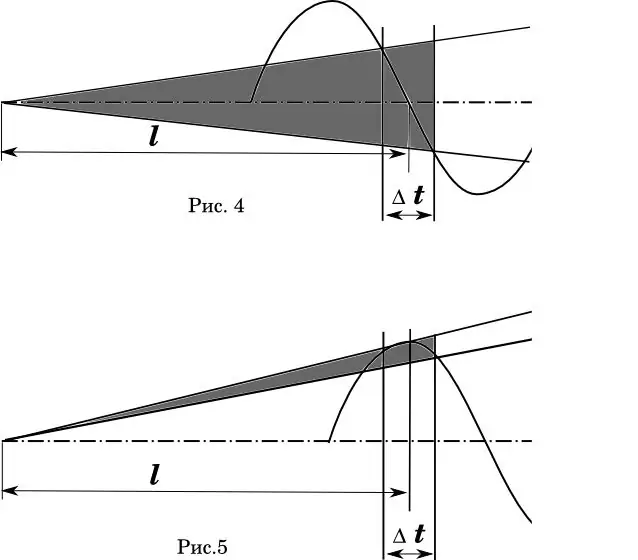
In Fig. 5 bleiben die Lauflänge und der Geschwindigkeitsfehler gleich. Aber die Phase der Tonnenbiegung wird so verschoben, dass die durchschnittliche Abfahrtszeit mit der maximalen Auslenkung des Rohrs zusammenfällt. Sind Kommentare überflüssig?
Nun, ist es die Kerze wert? Wie stark können die Abweichungen durch Schwingungen zweiter Ordnung sein? Ernst und sehr ernst. Nach Angaben des sowjetischen Professors Dmitry Alexandrovich Ventzel wurden in einem der Experimente folgende Ergebnisse erzielt: Der Radius der Medianabweichung nahm bei einer Änderung der Lauflänge um nur 100 mm um 40% zu. Zum Vergleich: Eine hochwertige Laufbearbeitung kann die Genauigkeit um nur 20 % verbessern!
Schauen wir uns nun die Formel für die Schwingungsfrequenz an:
wo:
k - Koeffizient für Schwingungen zweiter Ordnung - 4, 7;
L ist die Lauflänge;
E ist der Elastizitätsmodul;
I ist das Trägheitsmoment des Abschnitts;
m ist die Masse des Rumpfes.
… und fahren Sie mit der Analyse und den Schlussfolgerungen fort.
Die offensichtliche Schlussfolgerung aus den Abbildungen 4-5 ist der Geschossgeschwindigkeitsfehler. Sie hängt von der Qualität des Pulvers und dessen Gewicht und Dichte in der Kartusche ab. Beträgt dieser Fehler mindestens ein Viertel der Zykluszeit, kann auf alles andere verzichtet werden. Erfreulicherweise haben Wissenschaft und Industrie hier eine sehr große Stabilität erreicht. Und für die Anspruchsvolleren (zB im Benchrest) gibt es alle Voraussetzungen für die Selbstmontage von Patronen, um die Auslösephase des Geschosses exakt an die Lauflänge anzupassen.
Wir haben also eine Patrone mit der geringstmöglichen Geschwindigkeitsschwankung. Die Lauflänge wurde anhand des maximalen Gewichts berechnet. Es stellt sich die Frage der Stabilität. Wir schauen uns die Formel an. Welche Variablen beeinflussen die Änderung der Schwingungsfrequenz? Lauflänge, Elastizitätsmodul und Masse. Der Lauf erwärmt sich während des Schießens. Kann die Lauflänge durch Wärme ändern, so dass die Genauigkeit beeinträchtigt wird. Ja und nein. Ja, da dieser Wert bei einer Temperatur von 200 °C im Hundertstelprozentbereich liegt. Nein, da die Änderung des Elastizitätsmoduls von Stahl bei gleicher Temperatur etwa 8-9% beträgt, ist sie bei 60 °C fast doppelt so groß. Das heißt, um ein Vielfaches höher! Der Lauf wird weicher, die Biegephase des Laufs verschiebt sich bis zum Austritt des Geschosses nach vorne, die Genauigkeit sinkt. Nun, was sagt ein nachdenklicher Analytiker? Er wird sagen, dass es unmöglich ist, im Kalt- und Heißmodus maximale Genauigkeit auf einer Lauflänge zu erreichen! Die Waffe kann mit kaltem oder heißem Lauf eine bessere Leistung haben. Dementsprechend werden zwei Waffenklassen erhalten. Eine ist für Hinterhaltsaktionen, wenn das Ziel vom ersten getroffen werden muss - "kalter" Schuss, da die Genauigkeit des zweiten aufgrund der unvermeidlichen Erwärmung des Laufs schlechter wird. Bei einer solchen Waffe besteht kein dringender Bedarf an Automatisierung. Und die zweite Klasse sind automatische Gewehre, deren Lauflänge an den heißen Lauf angepasst ist. In diesem Fall kann ein möglicher Fehlschuss aufgrund der geringen Genauigkeit eines Kaltschusses durch einen schnellen nachfolgenden heißen und genaueren Schuss ausgeglichen werden.
EF Dragunov kannte die Physik dieses Prozesses sehr gut, als er sein Gewehr konstruierte. Ich schlage vor, dass Sie sich mit der Geschichte seines Sohnes Alexei vertraut machen. Aber zuerst muss sich jemand das Gehirn brechen. Wie Sie wissen, näherten sich zwei Proben von Konstantinov und Dragunov dem Finale des Wettbewerbs für ein Scharfschützengewehr. Die Designer waren Freunde und halfen sich in allem gegenseitig. Das Gewehr von Konstantinov war also auf den kalten Modus "abgestimmt", das Gewehr von Dragunov auf "heiß". Um die Genauigkeit des Gewehrs des Rivalen zu verbessern, feuert Dragunov sein Gewehr mit langen Pausen ab.

Schauen wir uns die Formel noch einmal an. Wie Sie sehen, hängt die Frequenz auch von der Masse des Laufs ab. Die Masse des Rumpfes ist konstant. Aber harter Kontakt mit dem Vorderschaft erzeugt ein unvorhersehbares positives Feedback zum Lauf. Das System - Lauf-Vorder-Arm (Stütze) hat ein anderes Trägheitsmoment (ein Satz von Massen relativ zum Befestigungspunkt), was bedeutet, dass dies auch eine Phasenverschiebung verursachen kann. Aus diesem Grund verwenden Sportler eine weiche Unterstützung. Das gleiche Merkmal ist mit der Anwendung des Prinzips des "aufgehängten Laufs" verbunden, wenn der Vorderschaft der Waffe keinen harten Kontakt mit dem Lauf hat und nur im Bereich der Waffe starr daran befestigt ist Empfänger, und das zweite Ende berührt den Lauf entweder überhaupt nicht oder berührt durch ein federbelastetes Gelenk (SVD).
Letzter Gedanke. Die Tatsache, dass es mit der gleichen Lauflänge unmöglich ist, die gleiche Genauigkeit bei verschiedenen Temperaturen zu erreichen, ist ein guter Grund, sich den Kopf zu spannen. Es ist nur erforderlich, die Länge und/oder Masse des Fasses zu ändern, wenn sich die Temperatur des Fasses ändert. Ohne die Länge oder das Gewicht des Laufs zu verändern. Aus geisteswissenschaftlicher Sicht ist dies ein Paradox. Aus der Sicht eines Technikfreaks eine ideale Aufgabe. Das ganze Leben eines Designers ist mit der Lösung solcher Probleme verbunden. Die Sherlocks ruhen.






