- Autor Matthew Elmers [email protected].
- Public 2024-01-11 06:07.
- Zuletzt bearbeitet 2025-01-24 09:22.
In diesem Artikel werden wir versuchen, die Panzerdurchdringung der Geschütze der Schlachtschiffe Bayern, Rivenge und Pennsylvania sowie die vergleichbare Qualität deutscher, amerikanischer und britischer Panzer zu verstehen. Dies ist äußerst schwierig, da die Daten der amerikanischen 356-mm-, deutschen 380-mm- und britischen 381-mm-Kanonen sehr lückenhaft und unvollständig sind und sich manchmal widersprechen, aber wir werden es trotzdem versuchen.
Was genau ist das Problem? Mal sehen, wie die meisten Fans der Marinegeschichte (und nicht nur) die Rüstungsdurchdringung bestimmter Waffen vergleichen. Zum Beispiel: In einer Publikation, die sich beispielsweise englischen Dreadnoughts widmet, gibt es Informationen, dass ein britisches 381-mm-Geschoss des Ersten Weltkriegs 381-mm-Panzerplatten im Abstand von etwa 70 Kabeln durchbohrt hat. In einer anderen Ausgabe, die den bereits deutschen "Hauptstadt"-Schiffen gewidmet ist - dass ein ähnliches deutsches 380-mm-Geschoss eine 350-mm-Panzerung mit nur 67,5 Kabeln "bewältigt". Daraus scheint zu folgen, dass die englische Kanone mächtiger ist - genau dies ist die Schlussfolgerung.
In der Realität ist es jedoch sehr einfach, solche Daten zu vergleichen.
Werden die oben genannten Daten durch tatsächliches Schießen gewonnen oder werden sie mithilfe von Panzerungsdurchschlagstechniken berechnet? Wenn dies die Ergebnisse des tatsächlichen Schießens sind, waren die Bedingungen für beide Geschütze identisch? Wenn die Panzerungsdurchdringung rechnerisch ermittelt wurde, wurden dann die gleichen Methoden verwendet? Sind die gewonnenen Daten das Ergebnis der Arbeit von Spezialisten der zuständigen Ministerien und Abteilungen oder das Ergebnis von Berechnungen von Historikern, die zum Taschenrechner gegriffen haben? Es ist klar, dass im zweiten Fall die Genauigkeit viel geringer ist … Sie müssen nicht weit gehen, um Beispiele zu nennen: Nehmen wir die berühmte Monographie von S. Vinogradov, "Superdreadnoughts des zweiten Reiches" Bayern "und" Baden ". In Anhang Nr. 2 hat der angesehene Historiker zusammen mit V. L. Kofman macht viele Berechnungen, um die Fähigkeiten der Schlachtschiffe Rivenge und Bayern zu vergleichen. Aber leider genügt ein Blick in die Parametertabelle für 15-Zoll-Geschütze (S. 124) und wir werden sehen, dass nach Berechnungen angesehener Autoren eine englische 381-mm-Kanone mit einem Elevationswinkel von 20, 25 Grad hat eine Reichweite von nur 105 Kabeln, also etwa 19, 5 Tausend m, während Fremdquellen für die gleiche Anfangsgeschwindigkeit (732 m / s) und einen etwas geringeren Elevationswinkel (20 Grad) deutlich größere Entfernungen ergeben - 21, 3-21, 7 Tausend m Natürlich wirken sich solche Abweichungen von den tatsächlichen Werten jedoch am negativsten auf die Berechnungsergebnisse aus.
Aber selbst wenn die Quellen die Ergebnisse von Berechnungen von Spezialisten präsentieren, deren Genauigkeit zweifellos besteht, tritt ein weiterer Faktor auf, der den Vergleich erschwert: Hier geht es um die Qualität der Rüstung. Es ist klar, dass die gleichen Briten bei der Berechnung der Rüstungsdurchdringung beim Entwerfen eines bestimmten Dreadnoughts die entsprechenden Indikatoren der britischen Rüstung, der Deutschen - bzw. Deutschen usw. Und die Rüstungen verschiedener Länder mögen sich in der Haltbarkeit unterscheiden, aber das ist immer noch die halbe Miete: Schließlich wurde in einem einzigen Land die gleiche Krupp-Panzerung ständig verbessert. So stellt sich heraus, dass die Berechnungen von Artilleriesystemen, die zum Beispiel in England gemacht wurden und anscheinend für die gleiche Krupp-Panzerung, aber zu unterschiedlichen Zeiten erstellt wurden, unvergleichlich sein können. Und wenn wir dazu noch das fast vollständige Fehlen ernsthafter Arbeiten zur Entwicklung des Panzergehäuses in verschiedenen Ländern der Welt hinzufügen …
Im Allgemeinen ist ein mehr oder weniger zuverlässiger Vergleich der Panzerdurchdringung keine so einfache Aufgabe, wie es auf den ersten Blick erscheinen mag. Und freundlicherweise sollte sich ein Laie (der zweifellos der Autor dieses Artikels ist) diese Angelegenheit besser nicht annehmen. Aber leider - zu unserem großen Bedauern haben die Profis keine Eile, sich mit diesen Problemen zu befassen, also … wie sie sagen, schreiben wir in Ermangelung von gestempeltem Papier im Klartext.
Natürlich ist es nicht mehr möglich, die oben genannten Artilleriesysteme in Originalgröße zu testen, daher ist unser Schicksal Berechnungen. Und wenn ja, dann ist es notwendig, zumindest ein paar Worte zu den Formeln für die Rüstungsdurchdringung zu sagen. Wenn moderne Berechnungsmethoden veröffentlicht werden, dann wird in der Regel nur in geschlossenen Ausgaben und in der populären Literatur die Jacob-de-Marr-Formel angegeben. Es ist interessant, dass Professor der Marineakademie L. G. Goncharov nannte sie in seinem Artillerie-Lehrbuch von 1932 die Jacob-de-Marr-Formel. Diese Formel war neben vielen anderen zu Beginn des letzten Jahrhunderts weit verbreitet, und ich muss sagen, sie ist ziemlich genau - vielleicht sogar die genaueste unter ähnlichen Formeln dieser Jahre.
Seine Besonderheit liegt darin, dass es nicht physikalisch ist, also keine mathematische Beschreibung physikalischer Prozesse. Die Formel von De Marr ist empirisch, sie spiegelt die Ergebnisse des experimentellen Beschusses von Eisen- und Stahl-Eisen-Rüstungen wider. Trotz dieser "unwissenschaftlichen Natur" zeigte die Formel von de Marr eine bessere Annäherung an die tatsächlichen Ergebnisse des Schießens und auf Krupp-Panzer als andere gängige Formeln, und daher werden wir sie für Berechnungen verwenden.
Interessierte finden diese Formel im Anhang zu diesem Artikel, aber es besteht keine Notwendigkeit, jeden, der dieses Material liest, zum Verständnis zu zwingen - dies ist nicht erforderlich, um die Schlussfolgerungen des Artikels zu verstehen. Wir stellen nur fest, dass die Berechnung allen an der Geschichte der Militärflotten Interessierten sehr einfache und vertraute Konzepte verwendet. Dies sind die Masse und das Kaliber des Projektils, die Dicke der Panzerung, der Auftreffwinkel des Projektils auf die Panzerung sowie die Geschwindigkeit des Projektils beim Auftreffen auf die Panzerplatte. Allerdings konnte sich de Marr natürlich nicht auf die oben genannten Parameter beschränken. Denn die Durchschlagskraft eines Geschosses hängt nicht nur von seinem Kaliber und seiner Masse ab, sondern in gewissem Maße auch von seiner Form und der Qualität des Stahls, aus dem es besteht. Und die Dicke der Panzerplatte, die das Projektil überwinden kann, hängt natürlich nicht nur von der Leistung des Projektils, sondern auch von der Qualität der Panzerung ab. Daher hat de Marr einen speziellen Koeffizienten in die Formel eingeführt, der tatsächlich die angegebenen Eigenschaften von Panzerung und Projektil berücksichtigt. Dieser Koeffizient steigt mit zunehmender Panzerungsqualität und sinkt mit einer Verschlechterung der Form und Qualität des Projektils.
Tatsächlich liegt die Hauptschwierigkeit beim Vergleich der Artilleriesysteme verschiedener Länder genau auf diesem Koeffizienten, den wir in Zukunft einfach (K) nennen werden. Wir müssen es für jedes der oben genannten Tools finden - wenn wir natürlich ein einigermaßen korrektes Ergebnis erzielen möchten.
Nehmen wir also zunächst ziemlich weit verbreitete Daten zur Panzerdurchdringung der deutschen 380-mm / 45-Kanone "Bayern", wonach die Waffe in einer Entfernung von 12.500 m (die gleichen 67,5-Kabel) 350 mm durchdringen konnte Rüstung. Wir verwenden einen ballistischen Rechner, um die Parameter eines 750-kg-Projektils mit einer Anfangsgeschwindigkeit von 800 m / s zum Zeitpunkt des Aufpralls auf die Panzerung zu ermitteln: Es stellt sich heraus, dass ein solches Projektil auf eine streng vertikal positionierte Panzerplatte trifft ein Winkel von 10, 39 Grad, mit einer Geschwindigkeit von 505,8 m / sek. Ein kleiner Haftungsausschluss - wenn wir im Folgenden über den Auftreffwinkel des Projektils sprechen, meinen wir den sogenannten "Winkel von der Normalen". "Normal" ist, wenn das Geschoss streng senkrecht zu seiner Oberfläche, also in einem Winkel von 90 Grad, auf die Bonneplite trifft. Dementsprechend traf das Projektil in einem Winkel von 10 Grad.von der Normalen bedeutet, dass es in einem Winkel von 80 Grad auf die Platte auftrifft. zu seiner Oberfläche, abweichend von der "Referenz" um 90 Grad. um 10 Grad.
Aber zurück zur Panzerdurchdringung des deutschen Geschützes. Der Koeffizient (K) beträgt in diesem Fall ungefähr (auf die nächste ganze Zahl gerundet) 2.083 - dieser Wert sollte für Rüstungen aus der Zeit des Ersten Weltkriegs als ganz normal angesehen werden. Aber hier tritt ein Problem auf: Tatsache ist, dass die Datenquelle zur Panzerdurchdringung das Buch "Deutsche Großkampfschiffe des Zweiten Weltkriegs" ist, in dem die 380-mm / 45-Kanone der Bayern mit dem Hauptkaliber des Schlachtschiffs verglichen wurde "Bismarck". Und könnte es nicht sein, dass die Berechnung die Indikatoren der Krupp-Panzerung berücksichtigte, die in der Zeit zwischen den beiden Weltkriegen erstellt wurde und viel stärker war als die, die auf der Bayenne, Rivenge und Pennsylvania installiert war? Darüber hinaus berichtet die elektronische Enzyklopädie Navweaps, dass es Beweise dafür gibt, dass deutsche 380-mm-Granaten in einer Entfernung von 20.000 m 336-mm-Panzerplatten durchschlagen konnten, und wir sprechen von Rüstungen aus der Zeit des Ersten Weltkriegs.
Nun, wir glauben: Bei 20 km beträgt der Einfallswinkel 23,9 Grad, die Geschwindigkeit des Projektils auf der Panzerung beträgt 410,9 m / s und der Koeffizient (K) - einige unglückliche 1618, die nicht in die Panzerung passen Widerstandswerte zu allen Zeiten des Ersten Weltkriegs. Ein ähnliches Ergebnis bringt die in Deutschland hergestellte Krupp-Rüstung im Allgemeinen näher an eine homogene Panzerungsresistenz … Offensichtlich enthalten die Navweap-Daten eine Art Fehler.
Versuchen wir dann, eine andere Informationsquelle zu verwenden. Bisher haben wir die berechneten Daten verwendet und werden nun versuchen, sie mit den Ergebnissen tatsächlicher Tests der deutschen 380-mm / 45-Kanone zu vergleichen: Diese werden von S. Vinogradov in der oben erwähnten Monographie über die deutsche Sprache angegeben Schlachtschiffe.
Es beschreibt die Folgen von 3 Schüssen mit panzerbrechenden Geschossen gegen Panzerplatten mit einer Dicke von 200, 290 und 450 mm, wobei letztere für uns am interessantesten ist: Ein 734 kg schweres Projektil traf in einem Winkel von 0. auf die Panzerplatte (also bei 90 Grad zur Oberfläche) und mit einer Geschwindigkeit von 551 m/s 450 mm durch die Platte gestanzt. Ein ähnliches Ergebnis entspricht dem Koeffizienten (K) 1 913, wird jedoch tatsächlich etwas niedriger sein, da die Deutschen ihr Projektil bis zu 2 530 m hinter dem durchbohrten Hindernis gefunden haben, und - im Allgemeinen. Da leider keine Daten darüber vorliegen, wie viel von dieser Entfernung das Projektil durch die Luft geflogen ist, wie viel - auf dem Boden "geritten" ist, ist es absolut unmöglich, die von ihm nach dem Durchdringen der Panzerung gespeicherte Energie zu bestimmen.
Nehmen wir nun das britische Artilleriesystem 381 mm / 42. Leider sind die Daten zur Panzerungsdurchdringung eher vage: Zum Beispiel V. L. Kofman, es wird erwähnt, dass diese britischen Geschütze Panzerungen durchbohrten, die die Dicke ihres eigenen Kalibers in einem Abstand von etwa 70 Kabeln hatten. Aber mit welchem Projektil und mit welcher Anfangsgeschwindigkeit? Unter Berücksichtigung der Tatsache, dass die Referenz in der Monographie zum Schlachtkreuzer "Hood" enthalten ist und sich auf die Entstehungszeit dieses Schiffes bezieht, kann davon ausgegangen werden, dass es sich um eine 871 kg schwere Granate handelt. Hier stellt sich jedoch eine andere Frage: Die offizielle Anfangsgeschwindigkeit eines solchen Projektils betrug 752 m / s, aber einige Berechnungen der Briten wurden mit einer niedrigeren Geschwindigkeit von 732 m / s durchgeführt. Welchen Wert sollten wir also nehmen? Unabhängig davon, welche der angegebenen Geschwindigkeiten wir verwenden, der Koeffizient (K) schwankt jedoch zwischen 1 983 - 2 048 und ist höher als wir für den Wert (K) für das deutsche Geschütz berechnet haben. Es ist anzunehmen, dass dies für die Überlegenheit der Qualität der britischen Panzerung gegenüber der deutschen spricht … oder war die geometrische Form des deutschen Projektils besser geeignet, um Panzerungen zu durchdringen? Oder vielleicht ist der springende Punkt, dass die Daten von V. L. Kofman sind berechnete Werte, aber würden britische Granaten in der Praxis ein besseres Ergebnis erzielen?
Nun, uns stehen Daten über die Ergebnisse des Beschusses des Schlachtschiffs "Baden" zur Verfügung.

Also, eine der britischen Granaten, die in einem Winkel von 18 Grad einschlägt. mit einer Geschwindigkeit von 472 m / Sek. "überwältigt" die 350-mm-Frontpanzerung des deutschen Hauptkaliberturms. Diese Daten sind umso wertvoller, da in diesem Fall nicht britische, sondern deutsche Panzer beschossen wurden, dh die Tests von 381-mm / 42- und 380-mm / 45-Geschützen sind somit in einem einzigen Koordinatensystem.
Leider helfen sie uns nicht allzu sehr. Wenn wir davon ausgehen, dass die englische Granate den deutschen Turm, wie sie sagen, „mit dem letzten Quäntchen Kraft“durchschlagen hat und wenn es 351 mm Panzerung gegeben hätte, wäre sie gescheitert, dann wäre sein (K) gleich 2.021 Interessant ist übrigens, dass S. Vinogradov angibt, dass das britische Projektil, das die 350-mm-Frontpanzerung des deutschen Turms durchschlug, nachträglich nicht gefunden wurde, aber tatsächlich sagt der Bericht etwas anderes aus - es explodierte, und es gibt eine Beschreibung, wohin die Fragmente im Turm geflogen sind.
Natürlich haben wir keinen absoluten Grund zu der Annahme, dass diese Durchschlagskraft die Grenze für ein 381-mm-Geschoss oder auch nur in der Nähe war. Dennoch ist nach einigen indirekten Hinweisen davon auszugehen, dass dies genau der Fall war. Ein weiterer Treffer-„Hinweis“darauf: Ein britisches 871-kg-Geschoss, das in einem Winkel von 11 Grad auf einen 350-mm-Barbet traf, konnte zwar ein Loch mit einem Durchmesser von 40 cm in die Panzerung bohren, gelangte jedoch nicht in den Barbet selbst und platzt bei der Überwindung der Rüstung. In diesem Fall trat der Treffer fast in der Mitte des Barbets auf, dh die Krümmung der Panzerplatte, wenn sie einen Einfluss hatte, war dies das Minimum.
Aus all dem kann man versuchen, einige Schlussfolgerungen zu ziehen, die jedoch aufgrund der Fragilität der Evidenzbasis natürlich sehr mutmaßlicher Natur sind.
Fazit 1: Deutsche Rüstungen während des Ersten Weltkriegs waren in Bezug auf die Haltbarkeit in etwa mit denen der Briten vergleichbar. Diese Schlussfolgerung gilt, wenn die Aussage von V. L. Kofman, dass die britische 381-mm / 42-Kanone in der Lage war, eine Panzerung ihres Kalibers um 70 kbt zu durchdringen, und wenn wir uns nicht in der Annahme irren, dass die Durchdringung der Frontplatte des deutschen Turms von 350 mm in einem Winkel von 18 Grad und einer Geschwindigkeit von 472 m / s … ist die Grenze oder sehr nahe an der Durchschlagsgrenze des britischen 381-mm-Projektils.
Fazit 2. Anscheinend sorgten Form und Qualität des deutschen 380-mm-Projektils für eine bessere Panzerdurchdringung als das englische. Basierend auf den obigen Daten können wir davon ausgehen, dass der Koeffizient (K) des britischen 381-mm-Projektils beim Abfeuern auf deutsche Panzerung etwa 2.000 betrug, während das deutsche 380-mm-Projektil etwa 1.900 betrug Der Panzerwiderstand britischer und deutscher Panzerung ist ungefähr gleich, es ist offensichtlich, dass der einzige Grund für den niedrigeren Koeffizienten (K) nur das Projektil selbst sein kann.
Warum könnte eine deutsche Hülle besser sein? Sein Kaliber ist mit einem Millimeter etwas kleiner, aber das kann natürlich kaum einen nennenswerten Einfluss haben. Die Berechnung zeigt, dass bei gleicher Masse (750 kg) eine Kaliberänderung um 1 Millimeter zu einer Erhöhung der Panzerdurchdringung um 1,03 Millimeter führt. Das deutsche Projektil ist auch kürzer - seine Länge betrug 3,5 Kaliber, während die Länge des britischen "Greenboy" 4 Kaliber beträgt. Es kann auch andere Unterschiede gegeben haben. Dabei spielt natürlich die Qualität des Stahls, aus dem das Geschoss besteht, eine große Rolle.
Berechnen wir nun die Panzerdurchdringung der deutschen und britischen Geschütze für eine Entfernung von 75 Kabeln - eine allgemein akzeptierte Entfernung für eine Entscheidungsschlacht, bei der man mit genügend Treffern rechnen konnte, um ein feindliches Linienschiff zu zerstören.
In der angegebenen Entfernung trafen 871 kg einer britischen 381-mm / 42-Kanonengranate, die mit einer Anfangsgeschwindigkeit von 752 m / s abgefeuert wurde, in einem Winkel von 13,05 Grad auf die vertikal positionierte Panzerplatte und ihre Geschwindigkeit "auf der Platte". war 479,6 m / s … Bei (K) = 2.000 betrug nach der Formel von Jacob de Marr die Panzerungsdurchdringung des britischen Projektils 376, 2 mm.
Bei der deutschen Shell ist alles etwas komplizierter. Wenn unsere Schlussfolgerung, dass es das Englische in Bezug auf die Panzerdurchdringung übertraf, richtig ist, dann waren die Fähigkeiten der deutschen 380-mm / 45-Kanone an 75 Kabeln der englischen 15-Zoll-Kanone sehr nahe. In dieser Entfernung traf das deutsche 750-kg-Geschoss das Ziel in einem Winkel von 12,42 Grad mit einer Geschwindigkeit von 482,2 m / s, und bei (K) gleich 1.900 betrug die Panzerungsdurchdringung 368,9 mm. Wenn sich der Autor dieses Artikels jedoch immer noch irrt und es sich bei der deutschen Waffe lohnt, den gleichen Koeffizienten wie bei der englischen Waffe zu verwenden, sinken die Fähigkeiten des 380-mm-Projektils auf 342,9 mm.
Laut dem Autor liegt die Panzerungsdurchdringung des deutschen Projektils jedoch am nächsten bei 368, 9 mm (immerhin ergab das praktische Schießen einen Koeffizienten von 1 913, obwohl das Projektil dann 2,5 km flog), aber die Panzerungsdurchdringung des englischen Projektils kann etwas niedriger berechnet werden. Generell kann davon ausgegangen werden, dass die britischen und deutschen Artilleriesysteme in einem Abstand von 75 Kabeln in Bezug auf die Panzerdurchdringung durchaus vergleichbar sind.
Aber mit der amerikanischen 356 mm / 45-Kanone wurde alles viel interessanter. Die zuvor zitierten Daten für Granaten mit einem Gewicht von 680 kg sind in der russischsprachigen Literatur als kanonisch anzusehen.
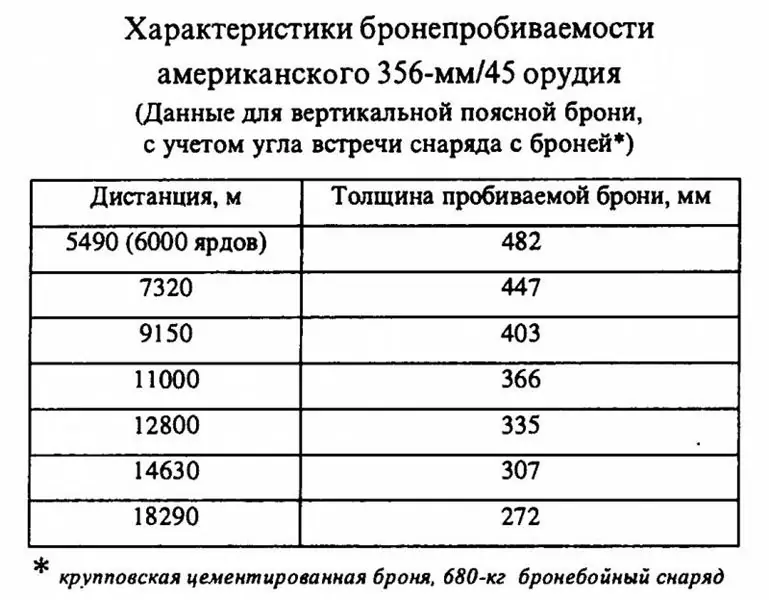
Tatsächlich scheinen die darin angegebenen Werte zu völlig offensichtlichen Schlussfolgerungen zu führen: Wenn selbst die 680-kg-Granaten, die nach 1923 in den Vereinigten Staaten auftauchten, in der Panzerungsdurchdringung ihren 380-381-mm-Europäern unterlegen sind " Kollegen", was dann wirklich über die früheren 635 kg-Granaten spricht, die mit 356-mm-Artillerie amerikanischer Dreadnoughts ausgestattet waren! Sie sind leichter, was bedeutet, dass sie im Flug schneller an Geschwindigkeit verlieren, während ihre Anfangsgeschwindigkeit schwerere Granaten nicht überstieg, und in Bezug auf Form und Qualität sollte die Munition von 1923 einen Vorteil haben. Dass die amerikanischen "Pennsylvania" zum Zeitpunkt ihrer Indienststellung den britischen und deutschen Dreadnoughts in der Panzerungsdurchdringung unterlegen waren, ist unübersehbar. Nun, es ist offensichtlich, nicht wahr?
Dies ist genau die Schlussfolgerung des Autors, wenn er die Fähigkeiten amerikanischer 14-Zoll-Geschütze im Artikel "Standard"-Schlachtschiffe der USA, Deutschlands und Englands berücksichtigt. Amerikanisches "Pennsylvania"". Und dann nahm er einen Taschenrechner …
Tatsache ist, dass die Berechnung nach der de Marra-Formel ergab, dass die amerikanischen 356-mm / 45-Geschütze die in der Tabelle angegebene Panzerungsdurchdringung mit einem Koeffizienten (K) von 2.317 hatten! Mit anderen Worten, die in der Tabelle aufgeführten amerikanischen 680-kg-Geschosse zeigten die Ergebnisse, wenn sie einer Panzerung ausgesetzt waren, die nicht in der Ära des Ersten Weltkriegs hergestellt wurde, sondern an viel späteren und haltbareren Proben.
Es ist schwer zu sagen, wie stark die Stärke des Panzerschutzes in der Zeit zwischen dem ersten und zweiten Weltkrieg zugenommen hat. In russischsprachigen Quellen gibt es nur kurze und oft widersprüchliche Hinweise auf diese Frage, aufgrund derer davon ausgegangen werden kann, dass die Stärke der Krupp-Panzerung um etwa 20-25% zugenommen hat. So wird für großkalibrige Granaten der Ära der Ersten Welt das Wachstum des Koeffizienten (K) von 1.900 - 2.000 auf 2.280 - 2.500 betragen, aber hier muss daran erinnert werden, dass die Qualität des Panzerschutzes steigt Natürlich ist die Qualität der Granaten auch gestiegen und daher für schwere Munition des Zweiten Weltkriegs (K) möglicherweise geringer. Daher sieht (K) in Höhe von 2.317 für Nachkriegsgranaten, natürlich verbessert unter Berücksichtigung der früheren Erfahrungen, ziemlich organisch aus, aber für die Panzerung der Ära des Zweiten Weltkriegs nicht die erste.
Aber indem wir den Koeffizienten (K) für die amerikanischen 680-kg-Granaten auf das Niveau von 2.000 setzen, dh indem wir die Qualität des Panzerschutzes in die Zeit des Ersten Weltkriegs bringen, erhalten wir für eine Entfernung von 75 Kabeln eine Panzerung Durchschlagshöhe von 393,5 mm, dh höher als die der britischen und deutschen 15-Zoll-Geschütze!

Die Umrechnung auf 635 kg Projektil ergibt eine sehr unbedeutende Korrektur - der ballistische Rechner zeigte dies in einem Abstand von 75 Kabeln mit einem Einfallswinkel von 10, 82 Grad. und die Geschwindigkeit "auf der Panzerung" 533, 2 m bei (K) gleich 2.000, das amerikanische Projektil durchdringt die Panzerung der Ära des Ersten Weltkriegs, 380 mm dick, also deutlich mehr als das eigene Kaliber!
Andererseits ist es durchaus möglich, dass eine solche Berechnung noch nicht ganz richtig ist. Tatsache ist, dass nach einigen Berichten der Koeffizient (K) für dieselbe Panzerung mit zunehmendem Kaliber des Projektils abnimmt. So beträgt zum Beispiel in unseren Berechnungen der Höchstwert (K) für das deutsche 380-mm / 45-Artilleriesystem, der durch Berechnung erhalten und in Quellen veröffentlicht wurde, 2.083. Gleichzeitig sind die Berechnungen für das deutsche 305-mm / 50 Kanonen, die auf Schiffen der Kaiserlichmarine ab Helgoland installiert wurden, geben die Daten aus Quellen zur Panzerdurchdringung (K) auf dem Niveau von 2.145 an, dementsprechend ist es möglich, dass die 356-mm / 45-Kanonen (K) = 2.000 Wir nahmen zur Berechnung der Panzerdurchdringung amerikanischer Geschütze noch zu klein an.
Darüber hinaus hat der Autor leider keine "Anhaltspunkte", um die Panzerungsresistenz der amerikanischen Krupp-Panzerung mit ihren europäischen Pendants zu vergleichen. Es bleibt nichts anderes übrig, als ihn mit deutschem und englischem Rüstungsschutz gleichzusetzen, obwohl dies natürlich nicht der Fall sein kann.
Fassen wir all diese ziemlich chaotischen Daten zusammen. Unter Berücksichtigung der Fehler der bei den Berechnungen verwendeten „Methoden“kann mit hoher Wahrscheinlichkeit davon ausgegangen werden, dass Die Panzerdurchdringung des vertikalen Panzerschutzes der Hauptkaliberkanonen der Schlachtschiffe Rivenge, Bayern und Pennsylvania im Abstand von 75 Kabeln war ungefähr gleich und betrug ungefähr 365-380 mm.
Trotz einer Reihe von Annahmen erlauben uns die uns vorliegenden Daten immer noch, einige Rückschlüsse auf den vertikalen Panzerschutz zu ziehen. Aber mit dem Durchbrechen von horizontalen Barrieren, die gepanzerte Decks sind, ist alles viel komplizierter. Tatsache ist, dass Jacob de Marr sich leider überhaupt nicht die Mühe gemacht hat, eine Formel zur Bestimmung der Stärke der horizontalen Verteidigung zu erstellen. Seine an moderne Panzerung angepasste Grundformel ist nur für die Berechnung von zementierten Panzern mit einer Dicke von über 75 mm geeignet. Diese Formel ist in Anhang Nr. 1 zu diesem Artikel angegeben, und alle vorherigen Berechnungen in dem Artikel wurden mit ihr durchgeführt.
Aber die Schiffsdecks dieser Jahre wurden nicht durch zementierte (heterogene), sondern durch homogene Panzerungen geschützt, denen eine oberflächengehärtete Schicht fehlte. Für solche Panzerung (aber - vertikal eingebaut!) wird eine andere Formel verwendet, die zur Bewertung von nicht zementierten Panzerplatten mit einer Dicke von weniger als 75 mm bestimmt ist und in Anhang Nr. 2 angegeben ist.
Ich möchte darauf hinweisen, dass diese beiden Formeln aus einer mehr als seriösen Quelle stammen: „Der Kurs der Marinetaktik. Artillerie und Rüstung 1932, Autor - Professor der RKKA Naval Academy L. G. Goncharov, einer der führenden Experten der Vorkriegs-UdSSR auf dem Gebiet der Marineartillerie.
Und leider ist keine davon geeignet, die Dauerhaftigkeit eines horizontalen Schutzes zu beurteilen. Wenn wir die Formel für zementierte Panzerung verwenden, erhalten wir bei einem Abstand von 75 Kabeln eine spärliche Panzerdurchdringung: 46,6 mm für 381 mm / 42 britische, 39,5 mm für 380 mm / 45 deutsch und 33,8 mm für 356 mm / 45 amerikanisch Waffen. Wenn wir die zweite Formel für nicht zementierte Panzerung verwenden, erhalten wir, dass bei einem Treffer in einem für eine Entfernung von 75 Kabeln typischen Winkel alle drei Artilleriesysteme leicht eine 74-mm-Panzerplatte durchdringen und danach einen enormen Vorrat an kinetischer Energie behalten - zum Beispiel das englische 381-mm, ein Projektil, das eine Panzerung dieser Dicke in einem Abstand von 75 Kabeln durchdringt, hat eine Geschwindigkeit von 264,5 m / s, während seine Geschwindigkeit 482,2 m / s beträgt. Wenn wir die Begrenzung der Dicke der Panzerplatte ignorieren, stellt sich heraus, dass das britische 381-mm-Geschoss nach obiger Formel in der Lage ist, Deckpanzerungen mit einer Dicke von über 180 mm zu durchdringen! Was natürlich völlig unmöglich ist.
Wenn wir uns auf die Testergebnisse des Schlachtschiffs der Bayern-Klasse beziehen, werden wir sehen, dass die panzerbrechenden britischen 871 kg-Granaten zweimal die horizontale Panzerung der Türme mit einer Dicke von 100 mm in einem Winkel von 11 Grad trafen, was einem Abstand von 67,5 Kabeln für ein Projektil mit einer Anfangsgeschwindigkeit von 752 m / s und 65 Kabeln entspricht - für ein Projektil mit einer Anfangsgeschwindigkeit von 732 m / s. Beide Male war die Rüstung nicht durchbohrt. Aber in einem Fall machte das Projektil, das abprallte, eine Nut in der Panzerung mit einer Tiefe von 70 cm, dh die Platte war sehr stark gebogen. Und im zweiten, obwohl die Granate wieder abprallte, war die Panzerung nicht nur um 10 cm konkav, sondern auch zerrissen.

Die ähnliche Art des Schadens deutet darauf hin, dass die deutsche 100-mm-Panzerung zwar in den angegebenen Entfernungen Schutz bot, aber wenn nicht an der Grenze des Möglichen, dann doch sehr nahe daran war. Die Berechnung nach der Formel für zementierte Panzerung ergibt jedoch eine Panzerdurchdringung von nur 46,6 mm in größerer Entfernung, wo der Einfallswinkel höher ist, und dementsprechend wäre es für das Projektil einfacher, die Deckpanzerung zu durchdringen. Das heißt, nach der Formel stellt sich heraus, dass das 100-mm-Deck scherzhaft und mit großem Sicherheitsspielraum englische Granaten widerspiegeln sollte - die Praxis bestätigt dies jedoch nicht. Gleichzeitig stellt sich nach Berechnungen mit der Formel für nicht zementierte Panzerung heraus, dass die Dächer des Badener Hauptkalibers leicht hätten durchschlagen werden müssen, und dies - bei einem großen Vorrat an Granatenenergie - was wiederum nicht der Fall ist durch die Praxis überhaupt bestätigt.
Ich muss sagen, dass solche Ungenauigkeiten in den Berechnungen eine völlig logische Erklärung haben. Wie bereits erwähnt, sind die Formeln von de Marr keine mathematische Beschreibung physikalischer Prozesse, sondern nur eine Fixierung der Muster, die beim Testen von Rüstungen erhalten wurden. Aber vertikaler Panzerschutz, nicht horizontal, wurde getestet, und es ist nicht verwunderlich, dass die Muster in diesem Fall einfach nicht mehr funktionieren: Bei horizontal angeordneten Panzern, in die die Granaten in einem sehr kleinen Winkel zu ihrer Oberfläche einschlagen, sind natürlich ganz anders.
Der Autor dieses Artikels stieß "im Internet" auf Meinungen, dass die Formeln von de Marr bei Abweichungswinkeln von der Normalen von nicht mehr als 60 Grad, dh von 30 Grad zur Oberfläche der Platte und mehr, effektiv funktionieren. Es ist davon auszugehen, dass diese Einschätzung der Wahrheit sehr nahe kommt.
Wir müssen daher mit Bedauern feststellen, dass der dem Autor zur Verfügung stehende mathematische Apparat keine verlässlichen Berechnungen des horizontalen Schutzwiderstandes der Schlachtschiffe Rivenge, Bayern und Pennsylvania erlaubt. In Anbetracht dessen wird es schwierig sein, die in verschiedenen Quellen angegebenen Daten zur Panzerdurchdringung horizontaler Panzerung zu verwenden - sie basieren in der Regel alle auf den gleichen Berechnungen nach den Formeln von de Marr und sind falsch.






